Sudoku

Writing a program to solve any possible Sudoku riddle can rather easily be done using the Constraint Satisfaction Problem (CSP). By adding only a few constraints one can solve even the hardest Sudoku in no time. We created two different approaches and let them run against each other.

Domain Adaption

In this approach we focused on the adaption of the domain, which means that we only added the all different constraints that each number can only occur once. To insert the existing variables, we restricted the domain of the field to the given number.

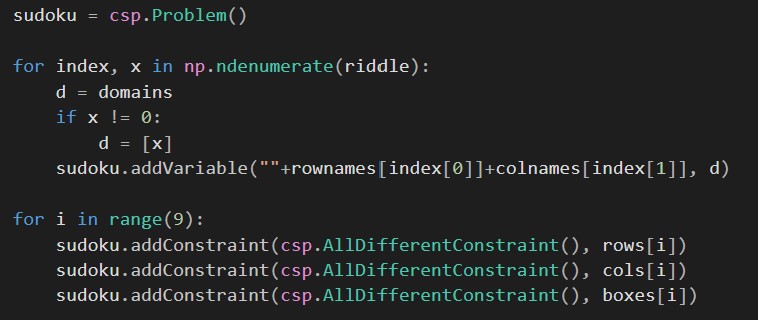
Constraint Addition

In contrary to the solution that has been discussed before, in this approach we add another constraint instead of reducing the domain for existing numbers. this constraint consists of a lambda function which is added to each predefined variable and limits its assignment to the given number.

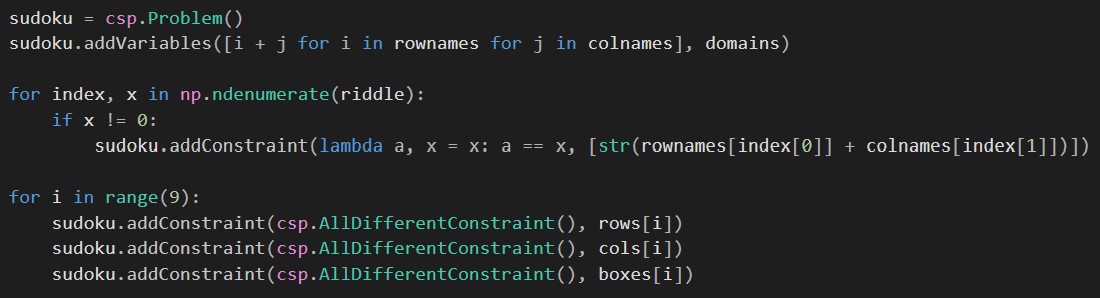
Comparison

Average Time over 10'000 iterations for standard and 100 iterations for hardest

Approach	Average Time per Standard game [s]	Average Time per Hardest game [s]
Domain Adaption	0.01889	1.48596
Constraint Addition	0.01762	1.19333

The table above indicates, that the approach with the Domain Adaption is a bit slower than the Constraint Addition. Interestingly we can see that when adding the constraint for existing variables, the domain for these is restricted after solving the riddle. Seeing that one would expect that the Domain Adaption is faster than Constraint Addition, but that's not the case. Even if the difference is in the range of 0.001 seconds it is clear that such a small change can influence the performance significantly. For more difficult sudoku puzzles the difference will be larger as it can be seen in the case of the hardest sudoku game.

The Hardest Sudoku

In 2012, Finnish mathematician Arto Inkala claimed to have created the "World's Hardest Sudoku".

Hardest Sudoku Starting Position

Hardest Sudoku Solution solved with CSP

Dragnet

There have been charges of insider trading against Katarina Quandt. The BigCompany AG held a board meeting on 12.02.2017 where they decided to launch a large share-buyback program in February of 2017. Shortly after this decision on 23.02.2017 Katarina Quandt bought vast amounts of shares from the BigCompany AG which lead us to believe that she had insider information about the program. To help solve the crime investigations are started using a dragnet, to see which company board member could have leaked the information.

Implementation

To create a dragnet using Datalog is a challenge! We have taken it up and created a dragnet to analyse calls and texts between people of a company. In this part of the blog we will go into depth how our dragnet works and explain what purpose which code-element fulfils. The terms 'knows', 'called' and 'texted' have already been with the information of the calls and texts issued by the suspects and their acquaintances in February 2017.

Knowing

This first part simply describes that if X knows Y, Y also knows X meaning knowing someone is bi-directional. A connection exists, if a there is a path of people, where one person knows the next one until the target Y is reached.

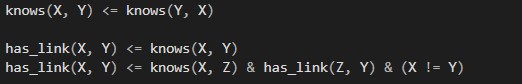
Paths

The term 'get_all_paths' uses recursion to find the path from X to Y. It checks that X is not equals Y and checks that Y is not already in the list, as without these it would create infinite loops. In get short paths, one can search for paths that are limited in the number of links, by defining constraints for L. For example get_short_paths("Berta", Y, P, L) & (L < 5) would return all paths from Berta to persons that are within a range of 5 links.

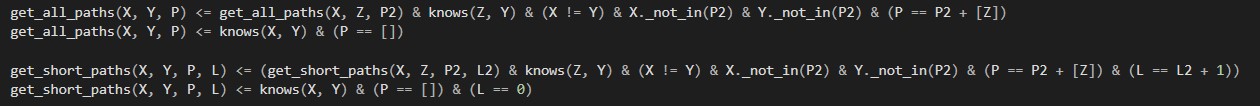
Dated Links

Previously the dates of the calls and the texts have been ignored. These informations will now be used in the further steps.

Dated links are working quite similar to the previous 'has_link' therm. The difference here is, that an additional rule is introduced. For a dated link to exist the contact from X to Y need to be in a descending date. If X had contact with Z after Z had contact with Y, Y cannot know the information X had. This model is a bit simplified as we're only checking the date and not the time, but the concept stays the same.

Dated Paths

For the dated paths we implement a restriction that de date itself is within the range we are interested into. This can be achieved by connecting the 'get_all_paths' terms with the constraints for (D >= date_board_decision) & (D <= date_shares_bought). Furthermore this therm contains a variable A which stores the path of dates.

Results

In the tables below, you can see that the possible suspects differ when we also take the date into consideration. These board members are still only suspects, because with the data provided we cannot tell what information has beeen exchanged. There could also be more suspects, because a board member could also have met Katarina Quandt personally. Sadly for this case we don't have any evidence at hand. The investigation has to go on with more data.

Paths from board members to Quandt Katarina with Depth = 5

Board Member	Path
Eder Eva	Egerer Leni -> Scheunemann Dario -> Quandt Katarina
Eder Eva	Egerer Leni -> Walz Grit -> Kretzer Julian -> Scheunemann Dario -> Quandt Katarina
Michael Jill	Walz Grit -> Kretzer Julian -> Scheunemann Dario -> Quandt Katarina
Michael Jill	Egerer Leni -> Walz Grit -> Kretzer Julian -> Scheunemann Dario -> Quandt Katarina

Paths from board members to Quandt Katarina with respect to dates

Board Member	Path
Eder Eva	12.02.2017 -> Egerer Leni -> 13.02.2017 -> Scheunemann Dario -> 16.02.2017 -> Quandt Katarina
Eder Eva	12.02.2017 -> Egerer Leni -> 17.02.2017 -> Welling Isabelle -> 20.02.2017 -> Lass Rudolf -> 21.02.2017 -> Quandt Katarina
Eder Eva	12.02.2017 -> Egerer Leni -> 13.02.2017 -> Scheunemann Dario -> 13.02.2017 -> Goerke Ella -> 14.02.2017 -> Klingler Karlotta -> 19.02.2017 -> Leibold Thorge -> 21.02.2017 -> Edel Margrit -> 23.02.2017 -> Quandt Katarina