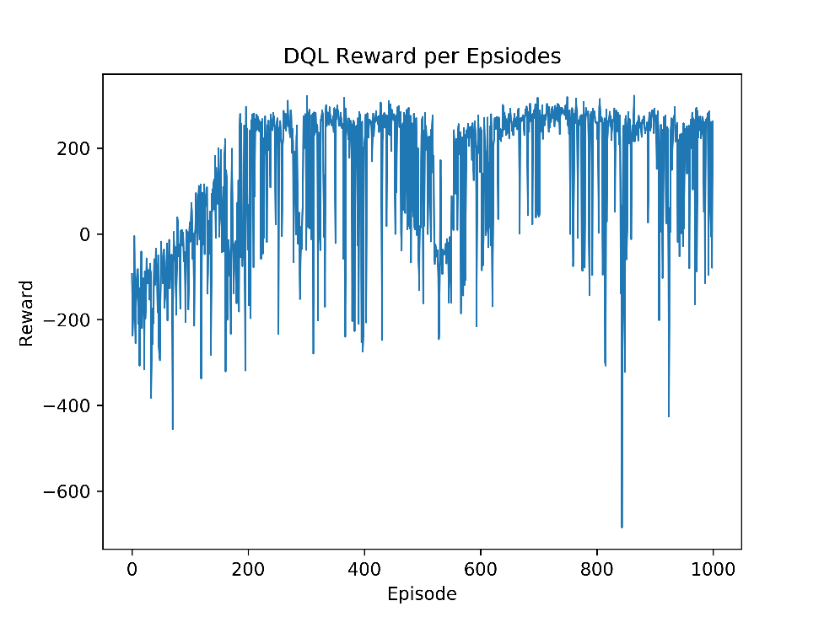
The aim of this lab is to implement a Reinforcement Learning algorithm that is able to provide a good solution for the Lunar Lander environment. We implemented three different approaches, namely a Deep Q Network (DQN), a REINFORCE and an Actor-Critic (AC) algorithm. We run all algorithms until the running reward exceeds the reward threshold (200 in this case). \begin{equation}reward_{running} = 0.005 * reward_{epsiode} + (1 - 0.05) * reward_{running}\end{equation} By doing so, we have a measure of how sample efficient each algorithm is. Additionally, we plot the received reward for each algorithm. Each environment is rolled out to a maximum of 10000 steps.

Deep Q Network

In DQN the agent predicts the reward for each possible action and picks the action (greedily) that promises the greatest reward, also called Q-value. The Q-value is defined as the following: \begin{equation}Q(s,a) = r(s,a) + \gamma * maxQ(s',a)\end{equation} Where $r(s,a)$ is the Reward of the next action in the current state, $\gamma$ is the reduction factor that diminishes the influence of rewards the farther they are in the future and $maxQ(s',a)$ is the greatest possible reward from the next steps. DQN uses experience replay, a technique where all selected actions are recorded, including the resulting reward. To improve performance, two networks are used where one is only update periodically to allow the training to be more stable.

Our implementation of the DQN algorithm scored the best with the following parameters

$\epsilon$-decay	0.99
$\gamma$	0.99
learning rate	0.001

The traineds models policy can be viewed in the following video:

REINFORCE

The REINFORCE algorithm is one of the first policy gradient algorithms in reinforcement learning. The difference between this algorithm and the Q-value algorithms is that it tries to learn a parametrized policy $\pi(s)$ instead of estimating the Q-values of state-action-pairs. This means, that the policy output is represented as a probability distribution of actions rather than a set of Q-value estimates. To get this probability distribution, the output is passed through a softmax activation. To update the weight of the network, the logvalues of the policy are multiplied by the total discounted received reward $G_t = R_t + \gamma R_{t+1} + \gamma^2R_{t+2} + ...$, to lift the future probability of good policy outputs. \begin{equation}\nabla J(\theta) = \nabla_\theta log \pi(s,a) * G_t\end{equation} Unlike the DQN-algorithm, REINFORCE does not use replay experience but updates the network after each environment rollout.
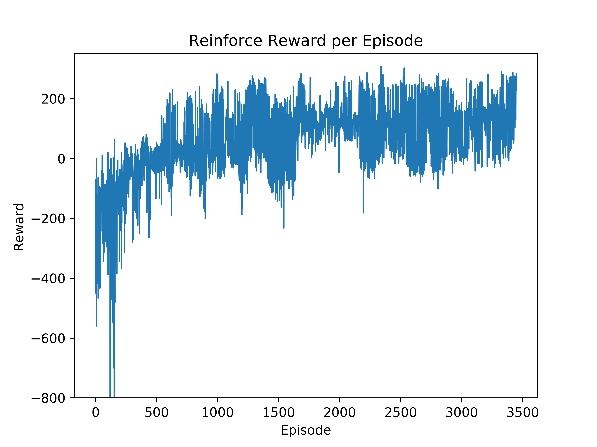
In the learning curve in Figure 2, we see that there are extreme outliners with negative scores exceeding -2000 in the early stages of the training. After the initial increase, the algorithm stabilizes and improves over time. Almost 3500 episodes are required to train a good solution with the REINFORCE algorithm and the chosen parameters.

Our implementation of the REINFORCE algorithm scored the best with the following parameters

$\gamma$	0.99
learning rate	0.003

The traineds models policy can be viewed in the following video:

Actor-Critic

Actor-Critic algorithms can be seen as a mixture between Policy-based and Value-based approaches. Two networks (or one network with two heads) are trained where the critic network estimates the value-function $V(s)$ and the actor network returns the policy $\pi(s,a)$.
Using the value-function and the total discounted reward $G_t$ per episode, it is now possible to calculate the so-called advantage $A$: \begin{equation}A = G_t - V(s)\end{equation} If the actual reward is larger than the one estimated by the value-function, this advantage is positive. If reward is smaller, it is negative. 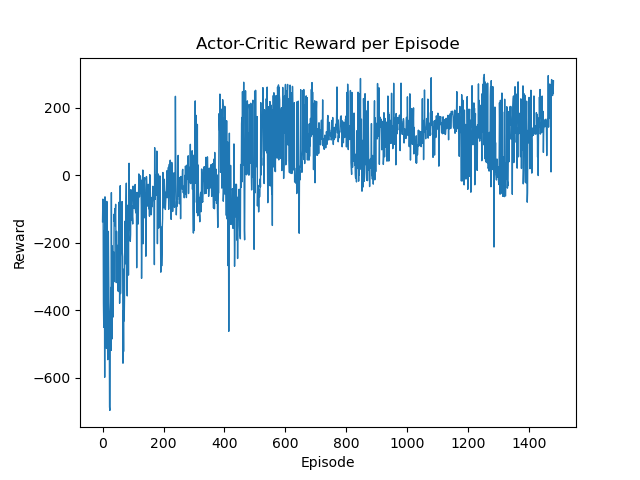This reward then gets used to amplify the update of the policy: \begin{equation}\nabla J(\theta) = \nabla_\theta log \pi(s,a) * G_t\end{equation} This helps the algorithm to perform positive policy updates for unexpectedly desirable outcomes and vice versa. We set the same reward threshold of 200 to evaluate the algorithm. While it does not reach the sample efficiency of DQN, it clearly outperforms the REINFORCE algorithm, which is expected as Actor-Critic is further developed algorithm of the family of policy gradient-based approaches.

Our implementation of the Actor-Critic algorithm scored the best with the following parameters

$\gamma$	0.99
learning rate	0.005

The traineds models policy can be viewed in the following video: