The game 2048 is a hard game to beat. As there are many random variables during play, one has a hard time to implement a good algorithm for it. We started off by implemented a heuristic algorithm and set the aim that it can reach 10'000 points in average.

Heuristic

Our first approach consisted of creating an algorithm which moved alternately down and right and as soon as he was stuck trying to find if the bottom row or the lefthand row was full and move in that direction. The idea behind this "Pretty Good" algorithm was to keep the highest tile in the bottom right corner. After a short time we realised that this strategy will not bear fruits as it's average score was around 4'000 points, so we discarded our algorithm and started over.
This time we made the "Check Score" algorithm which chose the turn that would lead to the greatest score, ignoring the random tile spawn. The scoring itself was a combination of different experiences that we obtained from the previous version. On one hand it gave penalties to moves that would lead to badly shaped boards and on the otherhand it gave bonus for same neighbours.
Built on the Check Score algorithm we build the "Hierarchical" algorithm which also did look two steps in the future in every possible direction (still ignoring the random tile spawn) and assessed the board at that stage. We valued the board by a score which was strongly depending on the position of the tiles. A better positioning of a tile lead to a higher factor. This factor will then be multiplied the value of the tile. 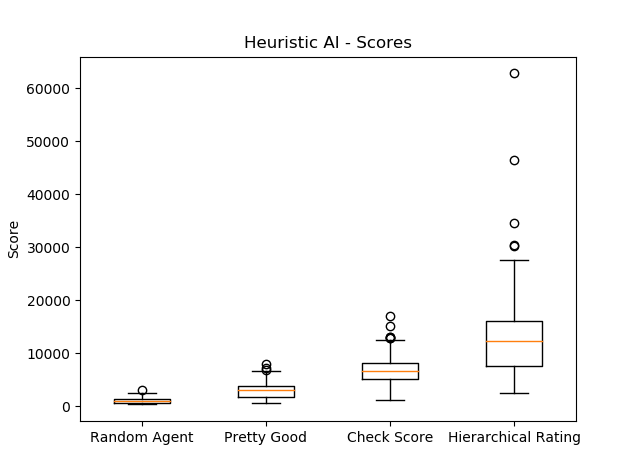A good position was the closeness to the bottom right corner, and the tile in the corner itself got an additional bonus, to force the algorithm to keep the highest value there. The board score distribution for this version looked like this:

Bonus distribution Hierarchical

These improvements got us way closer to our aim, overall the algorithm scored an average of 7'000 points.
We further improved it by giving a neighbourbonus which we had in the Check Score algorithm, for tiles of the same value and weighted empty tiles too, so the algorithm had more interest in merging tiles. This small tweaks finally pushed our algorithm slightly over the 10'000 points threshold.
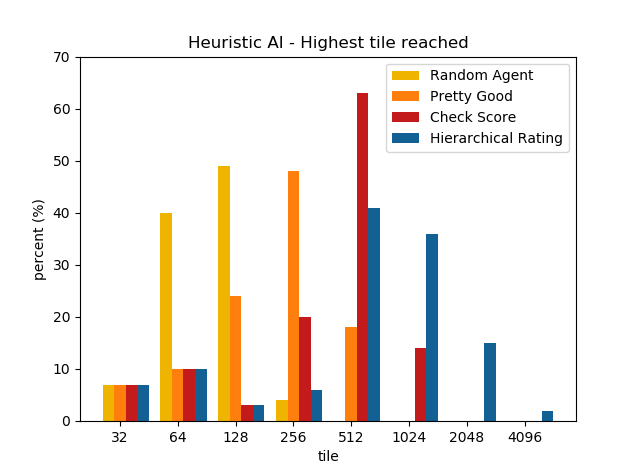
The following graphs show how the different heuristic algorithms did perform over 200 games and how they perform against the given random agent.

Comparison of the implemented heuristics

Algorithm Name	Highscore	Average Score	Highest Tile	Time Per Move [s]
Random Agent	2'960	1'052	256	0.010664
Pretty Good	8'012	4'121	512	0.003739
Check Score	17'080	6'975	1024	0.009889
Hierarchical Rating	62'800	14'752	4096	0.008578

Distribution of the heuristics score over 200 games

Distribution of the highest reached tiles of the heuristics over 200 games

Expectimax

As 2048 contains a random factor in regard of the randomly spawned 2 or 4 value tile, Expectimax is the most obvious approach to implement an AI. We used the Hierarchicals heuristics score function (called Heuristic in the following) to value the board, as well as an adaptive depth going from depth one to depth three depending on the number of empty tiles. This allowed us to speed up the early phase of the game, as depth 3 with our score function needed up to 20 seconds for a move, depending on the number of empty tiles after a move. As we urged for more speed, we also implemented multiprocessing into our AI that created a process for each top level move, in order to speed it up further. Thanks to the two mentioned measurements we achieved an average time per move of under one second. Overall the first iteration of our AI did alot better than the heuristic, it regularly won the game and the average score increased to 30'000 points. It was a good first step but we wanted to do better!
The next thing we tried was implementing a bonus if the neighbour was half as big, so that the AI can merge more smoothly. In contrary to what we expected, this measurement destroyed the algorithm and scored lower than the heuristic. We came up with the idea to distribute the factors like a snake and give the corner a hefty bonus, according to the following image:

Bonus distribution Improved Heuristic

The results showed further improvement in the average score up to 44'000 points. The problem was that the algorithm still did not stack the tiles in a perfect descending order. Sometimes small numbers where caught in the bottom left corner which disturbed the system and lead to big problems after the 4096 tile has been reached. Therefore we came up with the Snakey variation of the heuristic score system. In the Snakey variation we generated an array of big numbers with great distances between each other and in a descending order that would force the AI to fill up all the ranks in the bottom rows. This approach finally was the breakthrough we where looking for!
With an average score of 90'000 points it exceeded all previous implementations we made by far. Furthermore this variant was alot faster than previous iterations as it only needs to make one matrix multiplication instead of two for loops and multiple if statements.
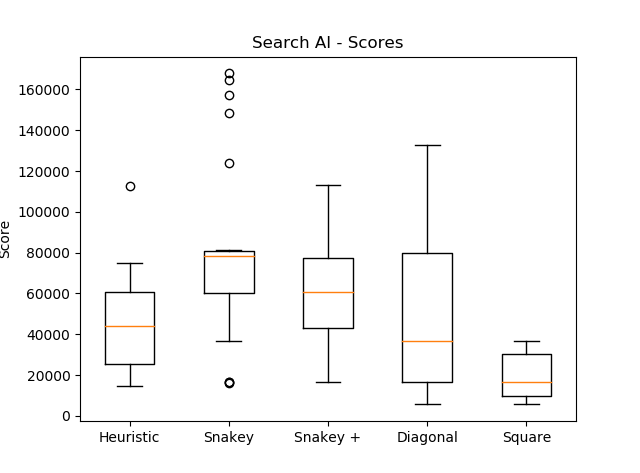
We tested out multiple other distributions, which we thought could work well with the same system as the Snakey. One was a diagonal decreasing distribution of the bonuses, another one was squares, and the last one was Snakey+ which also had a neighbourbonus implemented. At the end Snakey still was the most succesfull variation we created and if we wanted to improve it it just got worse. The score distribution for the different versions looked as follows:

Bonus distribution Snakey

Bonus distribution Diagonal

Bonus distribution Square

Conclusion

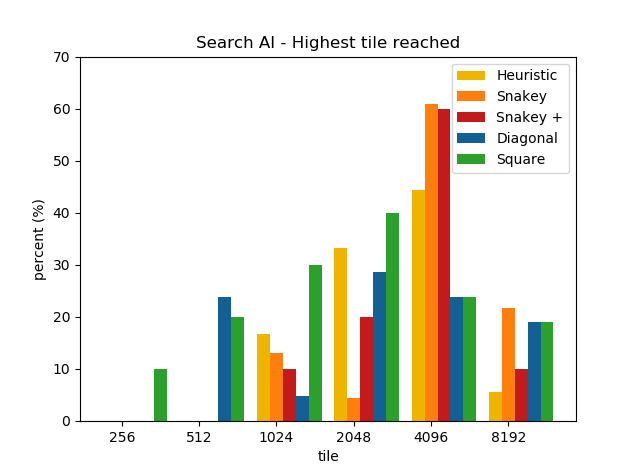
In the following table we listed the performance of each expectimax scoring function we developed, to compare them against each other.

Comparison of the implemented expectimax scoring functions

Algorithm Name	Highscore	Average Score	Highest Tile	Time Per Move [s]
Snakey	167'888	90'813	8192	0.58130573
Snakey+	113'180	68'555	8192	1.30097970
Diagonal	132'996	65'321	8192	0.54674995
Heuristic	112'776	44'194	8192	0.15212381
Square	36'772	19'658	2048	0.08806930

The following two graphs show how the score and the tiles have been distributed over 20 games. As one can see, is the Snakey scoring function mostly in the range between 60'000 to 80'000 points, which means that he often fails just before merging to the 8192. Whereas the Diagonal scoring function seems to have less problems merging to the 8192 tile when it even comes as far as the 4096 tile. This leads to the conclusion that in the Diagonal function the distribution of tiles seems to be better when the board is loaded with high tiles. A next step could be to combine the Snakey and Diagonal function, that the Snakey handles the part until the 4096 tile and then the Diagonal function takes over to reach an even higher score.

Distribution of the score over 20 games

Distribution of the highest reached tiles over 20 games

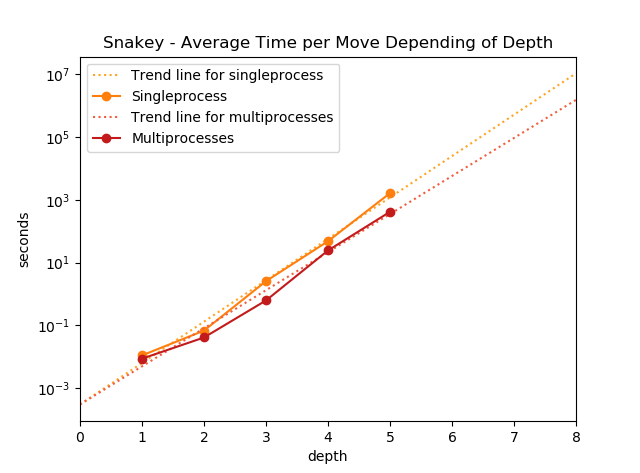
As a last step we analysed the speed of our AI and how much multiprocessing speeded the calculation up for different depths. We started always from the same board as seen on the graphic below and made three moves with every variation. The variations reached from depth one to depth five and once with multiprocessing enabled and once without. We calculated the average time per move and compared them to each other.
In conclusion we saw that multiprocessing is already a bit faster at depth one and nearly double as fast at depth two. As expected the performance boost increased quickly and at depth five multiprocessing was already four times faster than singleproccessing.

Startingboard of the time measurement

Depth	Singleprocess [s]	Multiprocess [s]
1	0.010971	0.008644
2	0.067817	0.040891
3	2.558497	0.620329
4	48.070847	24.369725
5	1641.396178	416.629117